In force voltage analogy velocity in mechanical system is equivalent to ___ in electrical system.
(c) Inductance (d) Capacitance
The transfer function is defined only for
(a) Linear time-invariant system (b) Nonlinear time-invariant system
(c) Nonlinear time variant system (d) Both a and b
Reduce the block diagram and find out the transfer function.
A system has transfer function (1-s)/(1+s). It is known as
(a) Low-pass system (b) High-pass system(c) All-pass system (d) None of these
The root locus starts from
(a) zeros and ends on poles (b) poles and ends on zeros(c) zeros and ends on infinity (d) poles and ends on infinity
How to find out the angle of asymptotes with the real axis in root locus analysis ?
The open-loop transfer function of a system is given by
then which of the following is true
(a) There will be a root locus in between -1 and -2
(b) There will be a root locus in between -5 and -2
(c) There will be a root locus in between -5 and -infinity
(d) Both a and c
If there are x number of poles and y number of zeros then how many root locus branches goes to infinity.
(a) 2x-y (b) 2y-xIf there are x number of poles and y number of zeros then how many root locus branches goes to infinity.
(c) x-y (d) x+y
Root locus is the locus of
(a) Open loop poles (b) Open loop zeros(c) Closed loop poles (d) Closed loop zeros
The starting point of root loci are
(a) Open loop poles (b) Open loop zeros
(c) Closed loop poles (d) Closed loop zeros
Root loci ends at
(a) Open loop poles (b) Open loop zeros(c) Closed loop poles (d) Closed loop zeros
There is system with transfer function
G(s)H(s)=k(s+3)/(s+1)(s+2)(s+5)
Find the point where the asymptotes of the root locus intersect the real axis G(s)H(s)=k(s+3)/(s+1)(s+2)(s+5)
(a) -2.5 (b) -2
(c) -1.5 (d) -1
If number of poles is denoted by p and number of zeros is denoted by z then the angle between the adjacent asymptotes in root locus analysis is
(a) 180/(p+z) (b) 90/(p-z)(c) 360/(p+z) (d) 360/(p-z)
Answers
1-b, 2-a, 3-a, 4-b, 5-b, 6-d, 7-b, 8-c, 9-c, 10-a
11-b, 12-a, 13-d


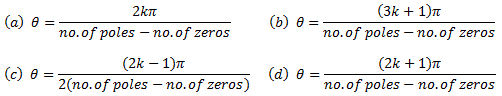

No comments:
Post a Comment